Mô hình phương trình cấu trúc tuyến tính riêng phần cơ bản (PLS-SEM) - bài 1

Mô hình phương trình cấu trúc tuyến tính riêng phần cơ bản (PLS -SEM) - bài 1

TÓM TẮT

SEM là một phương pháp thống kê mạnh mẽ, nó có thể xác định các mối quan hệ trong nghiên cứu khoa học xã hội mà những phương pháp khác không thể tìm thấy. Nội dung chính của bài giảng bao gồm:

1. Hiểu được ý nghĩa của mô hình cấu trúc tuyến tính (SEM) và mối quan hệ của nó với phân tích dữ liệu đa biến. SEM là một phương pháp phân tích dữ liệu đa biến thế hệ thứ hai. Phân tích dữ liệu đa biến liên quan đến ứng dụng của phương pháp thống kê đồng thời phân tích đa biến liên quan đến các cá nhân, các tổ chức, các sự kiện, các hoạt động, các tình huống,... SEM được sử dụng để khám phá hoặc khẳng định lý thuyết. Mô hình khám phá liên quan đến phát triển lý thuyết trong khi mô hình khẳng định kiểm định lý thuyết. Có hai loại SEM, một là dựa vào hiệp phương sai và còn lại dựa vào phương sai. CB-SEM được sử dụng để khẳng định (hoặc bác bỏ) lý thuyết. Mô hình cấu trúc tuyến tính dựa vào phương sai (PLS-SEM) thường được sử dụng cho những nghiên cứu khám phá và để phát triển lý thuyết.

 2. Mô tả các cân nhắc cơ bản trong việc áp dụng phân tích dữ liệu đa biến. Một số suy xét rất quan trọng khi áp dụng phân tích đa biến, bao gồm 5 yếu tố: (1) biến tổng hợp, (2) đo lường (3) thang đo, (4) mã hoá, và (5) phân phối dữ liệu. Một biến tổng hợp là sự kết hợp tuyến tính của một vài biến được chọn dựa trên các vấn đề nghiên cứu. Đo lường là một quá trình gán số cho một biến dựa trên tập hợp các quy tắc. Đo lường đa biến liên quan đến việc sử dụng một vài biến để đo gián tiếp một khái niệm nhằm nâng cao độ chính xác của phương pháp đo. Việc cải thiện độ chính xác trước mắt dựa trên giả định rằng sử dụng một số biến (các biến quan sát) để đo một khái niệm đơn thì nhiều khả năng đại diện cho tất cả các khía cạnh khác nhau của khái niệm và dẫn đến kết quả là việc đo lường khái niệm sẽ có giá trị nhiều hơn. Khả năng xác định các sai số đo lường bằng cách sử dụng phép đo lường đa biến còn giúp các nhà nghiên cứu có được phép đo lường chính xác hơn. Sai số đo lường là sự khác biệt giữa giá trị thật của biến và giá trị có được bởi phép đo lường. Thang đo là một công cụ định trước giá trị (con số) của câu trả lời dạng đóng (closed-ended) được sử dụng để có được một câu trả lời cho một câu hỏi. Có bốn loại thang đo lường: danh nghĩa, thứ bậc, khoảng, và tỷ lệ. Khi các nhà nghiên cứu thu thập dữ liệu định lượng có sử dụng thang đo, câu trả lời cho câu hỏi có thể hiển thị một phân phối có sẵn (định trước dạng trả lời). Các dạng phân phối phải luôn luôn được xem xét khi làm việc với SEM.

             3. Hiểu các khái niệm cơ bản của mô hình cấu trúc bình phương tối thiểu từng phần SEM (PLS-SEM). Mô hình đường dẫn là các biểu đồ được sử dụng hiển thị trực quan mối quan hệ của biến và giả thuyết, được kiểm tra khi mô hình cấu trúc tuyến tính được áp dụng. Có bốn yếu tố cơ bản phải hiểu khi sử dụng mô hình đường dẫn: (1) khái niệm nghiên cứu (construct), (2) biến đo lường (measured variable), (3) mối quan hệ (relationship), và (4) phần sai số (error term). Khái niệm nghiên cứu là những biến tiềm ẩn mà không thể đo một cách trực tiếp và thỉnh thoảng được gọi là các biến không quan sát được. Nó được biểu diễn trong mô hình đường dẫn bằng các hình tròn hoặc hình bầu dục. Các biến được đo một cách trực tiếp (dữ liệu thô) thường được gọi là biến chỉ báo hoặc biến quan sát và được thể hiện trong mô hình bằng các hình chữ nhật. Các mối quan hệ đại diện các giả thuyết trong mô hình đường và được hiển thị bằng các mũi tên đơn hướng (một chiều) cho thấy mối quan hệ dự báo hoặc nhân quả. Các phần sai số đại diện cho phương sai không được giải thích khi mô hình đường dẫn được ước lượng và được thể hiện bằng các hình tròn kết nối khái niệm nghiên cứu (nội sinh) và các biến đo lường (kết quả) bằng mũi tên một chiều. Khái niệm ngoại sinh và biến đo lường nguyên nhân không có phần sai số. Mô hình đường dẫn còn phân biệt giữa mô hình cấu trúc (bên trong) và mô hình đo lường (bên ngoài). Vai trò của lý thuyết rất quan trọng khi phát triển mô hình cấu trúc. Lý thuyết là tập hợp các giả thuyết có liên quan một cách hệ thống theo phương pháp khoa học, được sử dụng để giải thích và dự đoán kết quả. Lý thuyết đo lường chỉ rõ cách những biến tiềm ẩn không quan sát được (khái niệm nghiên cứu) được mô hình hoá. Biến tiềm ẩn có thể được mô hình hoá như nguyên nhân hoặc kết quả. Lý thuyết cấu trúc chỉ ra cách các biến tiềm ẩn không quan sát được liên quan đến nhau. Các biến tiềm ẩn được phân loại ra thành biến nội sinh hoặc ngoại sinh.

             4. Giải thích sự khác nhau giữa CB-SEM và PLS-SEM và khi nào sử dụng chúng. Như một thay thế cho CB-SEM, PLS-SEM nhấn mạnh các mục tiêu dự báo trong khi tương đồng về các nhu cầu cần thiết dữ liệu và đặc điểm của các mối quan hệ. PLS-SEM tối đa phương sai được giải thích của biến tiềm ẩn nội sinh bằng việc ước lượng các mối quan hệ mô hình riêng phần trong chuỗi lặp lại của hồi quy OLS. Ngược lại, CB-SEM ước lượng các tham số mô hình mà không có sự nhất quán giữa ước lượng và ma trận hiệp phương sai là nhỏ nhất. Thay vì tuân theo logic mô hình các yếu tố chung như CB-SEM, PLS-SEM tính toán các hợp nhất của các biến quan sát dùng làm đại diện cho các khái niệm trong nghiên cứu. PLS-SEM không bị hạn chế bởi vấn đề nhận dạng, ngay cả khi mô hình trở nên phức tạp - một tình huống mà thông thường hạn chế sử dụng CB-SEM - và không yêu cầu trong hầu hết các giả định phân phối. Hơn nữa, PLS-SEM có thể xử lý tốt hơn mô hình đo lường nguyên nhân và có lợi thế khi mẫu tương đối nhỏ. Các nhà nghiên cứu nên cân nhắc hai kỹ thuật SEM như bổ sung lẫn nhau và áp dụng kỹ thuật SEM nào phù hợp nhất cho mục tiêu nghiên cứu, đặc điểm dữ liệu và thiết lập mô hình.

CÁC THUẬT NGỮ CHÍNH

CB-SEM/Mô hình CB-SEM: xem Covariance-based structural equation modeling

Coding/Mã hoá: là gán số cho thang đo

Composite variable: biến số/ biến tổng hợp

Confirmatory applications/Các ứng dụng khẳng định: nhằm mục đích kiểm định thực nghiệm mô hình phát triển lý thuyết

Constructs/Khái niệm nghiên cứu (còn được gọi là biến tiềm ẩn): khái niệm trừu tượng, phức tạp và không thể quan sát trực tiếp bằng các (nhiều) biến quan sát. Khái niệm nghiên cứu được thể hiện trong mô hình đường dẫn bằng hình tròn hoặc hình bầu dục.

Covariance-based structural equation modeling CB-SEM/Mô hình cấu trúc tuyến tính dựa trên hiệp phương sai: được sử dụng để khẳng định (hoặc bác bỏ) lý thuyết. Việc này được thực hiện bằng cách xác định một theo mô hình lý thuyết đề xuất, có thể ước lượng ma trận hiệp phương sai cho một tập dữ liệu mẫu. 

Endogenous laten variables/ Biến tiềm ẩn nội sinh: chỉ được dùng như là các biến phụ thuộc, hoặc là cả biến độc lập và phụ thuộc trong mô hình cấu trúc.

Equidistance/Khoảng cách bằng nhau: được đưa ra khi khoảng cách giữa các điểm dữ liệu của một thang đo là giống hệt nhau.

Error terms/Phần sai số: phản ánh phương sai không thể giải thích trong khái niệm nghiên cứu và các biến quan sát khi mô hình đường dẫn được ước lượng.

Exogenous latent variables/Biến tiềm ẩn ngoại sinh: là các biến tiềm ẩn mà chỉ dùng như là các biến độc lập trong mô hình cấu trúc.

Exploratory/Khám phá: xem ứng dụng khám phá.

Exploratory/Ứng dụng khám phá: tập trung vào khám phá các mô hình dữ liệu và xác định các mối quan hệ.

First-generation techniques/Kỹ thuật thế hệ thứ nhất: là phương pháp thống kê truyền thống được sử dụng bởi các nhà nghiên cứu, chẳng hạn như hồi quy và phân tích phương sai.

Formative measurement model/Mô hình đo lường nguyên nhân: là một loại hình thiết lập mô hình đo lường trong đó hướng của mũi tên đi từ các biến quan sát tới khái niệm nghiên cứu, nêu ra giả định rằng các biến quan sát đo lường cho khái niệm nghiên cứu.

Indicators/Các biến quan sát: là những quan sát đo trực tiếp (dữ liệu thô), thường được gọi là biến đo lường (items) hoặc biến biểu thị (manifest), được trình bày trong mô hình đường dẫn bằng các hình chữ nhật.

Inner model/Mô hình bên trong: xem mô hình cấu trúc.

Interval scale/Thang đo khoảng: có thể được sử dụng để đưa ra một sự phân hạng và có một hằng số đo lường vì thế khoảng cách giữa các mốc của thang đo là bằng nhau.

Items/Các biến quan sát: xem Indicator

Latent variables/Các biến tiềm ẩn: xem Constructs

Manifest variables/Các biến quan sát: xem Indicators

Measurement/Sự đo lường: là quá trình gán các số cho một biến dựa trên một tập hợp các quy tắc.

Measurement error/Sai số đo lường: là sự khác biệt giữa giá trị thực sự của một biến và giá trị thu được bằng một phép đo.

Measurement model/Mô hình đo lường: là một yếu tố của mô hình đường dẫn có chứa các biến quan sát và mối quan hệ của chúng với các khái niệm nghiên cứu và cũng được gọi là mô hình bên ngoài trong PLS-SEM.

Measurement scale/Thang đo lường: là một công cụ với một số định trước các trả lời dạng đóng, được sử dụng để thu được một câu trả lời cho một câu hỏi.

Measurement theory/Lý thuyết đo lường: quy định cụ thể cách thức mà các biến tiềm ẩn được đo lường.

Multivariate analyses/Phân tích đa biến: là phương pháp thống kê phân tích đồng thời nhiều biến.

Multivariate measurement/Đo lường đa biến: liên quan đến việc sử dụng một số biến để gián tiếp đo lường một khái niệm.

Norminal scale/Thang đo danh nghĩa: là một thang đo lường trong đó các con số được gán nhằm xác định và phân loại các đối tượng (ví dụ, con người, công ty, sản phẩm, vv).

Ordinal scale/Thang đo thứ bậc: là một thang đo lường trong đó các con số được gán nhằm chỉ ra vị trí tương đối của đối tượng trong một dãy sắp xếp.

Outer model/Mô hình bên ngoài: xem Mô hình đo lường.

Partial least squares path modeling/Mô hình đường dẫn bình phương tối thiểu riêng phần: xem Mô hình cấu trúc tuyến tính bình phương tối thiểu riêng phần

Partial least squares structural equation modeling/Mô hình cấu trúc tuyến tính bình phương tối thiểu riêng phần: là một phương pháp dựa trên phương sai để ước lượng mô hình phương trình cấu trúc. Mục đích là để tối đa hóa sự giải thích của các biến tiềm ẩn nội sinh.

Path models/Mô hình đường dẫn: là các biểu đồ trực quan hiển thị các giả thuyết và các mối quan hệ của biến, được kiểm tra khi mô hình cấu trúc tuyến tính được áp dụng.

PLS regression/Hồi qui PLS: là một kỹ thuật phân tích, khám phá mối quan hệ tuyến tính giữa nhiều biến độc lập với một hoặc nhiều biến phụ thuộc. Trong mô hình hồi quy, nó tạo ra sự tổng hợp từ cả nhiều biến độc lập và biến phụ thuộc bằng cách phân tích thành phần chính.

PLS-SEM: xem Mô hình cấu trúc tuyến tính bình phương tối thiểu riêng phần

Ratio scales/Thang đo tỷ lệ: là mức cao nhất của đo lường bởi vì chúng có giá trị hằng số đo lường và điểm không (0) tuyệt đối; tỷ lệ có thể được tính toán bằng cách sử dụng các điểm thang đo.

Recursive model/Mô hình đệ qui (qui nạp): là mô hình đường dẫn PLS mà không có một vòng nhân quả của mối quan hệ giữa các biến tiềm ẩn trong mô hình cấu trúc (tức là, không có mối quan hệ vòng tròn).

Reflective measurement model/Mô hình đo lường kết quả: là một dạng mô hình đo lường trong đó hướng của mũi tên là từ khái niệm nghiên cứu đi đến các biến quan sát, chỉ ra giả định rằng khái niệm nghiên cứu gây ra sự đo lường (chính xác hơn, sự hiệp biến) của các biến quan sát.

Second-generation techniques/Kỹ thuật thế hệ thứ hai: khắc phục những hạn chế của kỹ thuật thế hệ đầu tiên, ví dụ, xét về góc độ tính toán sai số đo. SEM là kỹ thuật phân tích dữ liệu thế hệ thứ hai nổi bật nhất.

SEM: xem Mô hình cấu trúc tuyến tính.

Single-item constructs/Khái niệm nghiên cứu đơn biến: chỉ có một biến duy nhất để đo khái niệm nghiên cứu.

Statistical power/Độ nhạy thống kê: là xác suất để phát hiện mối quan hệ có ý nghĩa thống kê khi nó thực tế có ý nghĩa trong tổng thể.

Structural equation modeling/Mô hình cấu trúc tuyến tính: được sử dụng để đo lường các mối quan hệ giữa các biến tiềm ẩn.

Structural model/Mô hình cấu trúc: là một phần của mô hình đường dẫn PLS có chứa các khái niệm nghiên cứu cũng như các mối quan hệ giữa chúng. Nó cũng được gọi là mô hình bên trong của PLS-SEM.

Structural theory/Lý thuyết cấu trúc: quy định cụ thể cách các biến tiềm ẩn liên quan đến nhau. Đó là, nó chỉ ra các khái niệm nghiên cứu và các đường dẫn giữa chúng.

Theory/Lý thuyết: là một tập hợp các giả thuyết liên quan một cách hệ thống, phát triển theo các phương pháp khoa học có thể được sử dụng để giải thích và dự đoán kết quả và có thể được kiểm định bằng thực nghiệm.

Variance-based SEM/SEM dựa vào phương sai: xem Mô hình cấu trúc tuyến tính bình phương tối thiểu riêng phần

Variate/Biến: là sự kết hợp tuyến tính của nhiều biến số.

Các nhà nghiên cứu khoa học xã hội đã sử dụng các công cụ phân tích thống kê từ nhiều năm trước để mở rộng khả năng của mình nhằm phát triển, khám phá và khẳng định những nghiên cứu. Ứng dụng của các phương pháp thống kê thế hệ đầu như phân tích nhân tố và hồi quy chiếm ưu thế trong nghiên cứu nói chung từ năm 1980. Nhưng kể từ năm 1990, các phương pháp thế hệ thứ hai dần mở rộng quy mô một cách nhanh chóng và trong một số ngành nó đại diện cho gần 50% các công cụ thống kê được áp dụng trong các nghiên cứu thực nghiệm. Trong chương này, chúng tôi sẽ giải thích rõ những vấn đề cơ bản của các phương pháp thống kê thế hệ thứ hai, và thiết lập một nền tảng cho phép hiểu và áp dụng  một trong những công cụ mới nổi này, gọi tắt là mô hình cấu trúc tuyến tính bình phương tối thiểu từng phần (PLS-SEM).

MÔ HÌNH CẤU TRÚC TUYẾN TÍNH LÀ GÌ?

Phân tích thống kê là một công cụ thiết yếu cho các nhà nghiên cứu khoa học xã hội khoảng hơn một thế kỷ. Những ứng dụng của các phương pháp thống kê được mở rộng đáng kể bởi sự xuất hiện của phần cứng và phần mềm máy tính, đặc biệt trong những năm gần đây, với sự phổ biến của nhiều phương pháp nhằm tạo nên một giao diện thân thiện cho người dùng với sự chuyển giao khoa học công nghệ. Ban đầu, các nhà nghiên cứu dựa trên các phân tích về đơn biến và đa biến để hiểu và nắm bắt các mối quan hệ của dữ liệu. Sau đó, để hiểu rõ hơn các mối quan hệ phức tạp liên quan đến các hướng nghiên cứu trong khoa học xã hội hiện tại, việc ứng dụng của các phương pháp phân tích dữ liệu đa biến tinh vi hơn ngày càng cần thiết.

Phân tích đa biến bao gồm các ứng dụng của các phương pháp thống kê, và phân tích đồng thời nhiều biến. Các biến thường đại diện cho sự đo lường liên quan đến các cá nhân, công ty, sự kiện, hoạt động, tình huống... Các đo lường này thường được thu thập từ việc khảo sát hoặc quan sát, nó được sử dụng trong khi thu thập dữ liệu sơ cấp, nhưng cũng có thể được thu thập từ cơ sở dữ liệu của dữ liệu thứ cấp. Bảng 1.1 trình bày các dạng chính của các phương pháp thống kê liên quan đến phân tích dữ liệu đa biến.

BẢNG 1.1 Sơ đồ tổ chức của các phương pháp đa biến
	Khám phá chủ yếu	Khẳng định chủ yếu
Các kỹ thuật thế hệ đầu tiên	·         Phân  tích cụm ·         Phân tích nhân tố khám phá ·         Đo lường đa hướng	·         Phân  tích phương  sai ·         Hồi quy logistic ·         Hồi quy bội ·         Phân tích nhân tố khẳng định
Các kỹ thuật thế hệ thứ hai	·         Mô hình SEM sử dụng kỹ thuật bình phương tối thiểu từng phần PLS-SEM	·         Mô hình SEM sử dụng hiệp phương sai CB-SEM

Các phương pháp thống kê thường được sử dụng bởi các nhà khoa học xã hội thường được gọi là các kỹ thuật thế hệ thứ nhất (Fornell, 1982, 1987). Những kỹ thuật này được trình bày ở phần trên của Bảng 1.1, gồm có các phương pháp tiếp cận dựa trên hồi quy như hồi quy bội, hồi quy logistic và phân tích phương sai cũng như bao gồm phân tích nhân tố khám phá và phân tích nhân tố khẳng định, phân tích cụm, đo lường đa hướng. Khi áp dụng vào vấn đề nghiên cứu, các phương pháp này có thể được sử dụng cùng nhau để khẳng định lý thuyết hoặc xác định mô hình dữ liệu và các mối quan hệ. Cụ thể, chúng gọi là khẳng định khi kiểm định các giả thuyết của lý thuyết và khái niệm hiện có, và gọi là khám phá khi chúng tìm kiếm mô hình tiềm ẩn trong dữ liệu trong trường hợp không có hoặc chỉ có một ít kiến thức trước đó về sự liên quan của các biến.

Điều quan trọng cần lưu ý là sự phân biệt giữa khẳng định và khám phá không phải lúc nào cũng rõ ràng. Ví dụ, khi chạy phân tích hồi quy, các nhà nghiên cứu thường chọn các biến phụ thuộc và độc lập dựa trên các lý thuyết và khái niệm trước đó. Mục tiêu của phân tích hồi quy là kiểm định các lý thuyết và khái niệm này. Tuy nhiên, kỹ thuật cũng được sử dụng để khám phá các biến độc lập bổ sung chứng minh giá trị cho việc mở rộng các khái niệm đang được kiểm định. Những phát hiện này thường tập trung đầu tiên vào các biến độc lập có ý nghĩa thống kê trong việc dự đoán biến phụ thuộc (khẳng định nhiều hơn) và các biến độc lập có khả năng dự báo tốt hơn cho biến phụ thuộc (khám phá nhiều hơn). Một cách tương tự, khi phân tích nhân tố khám phá được áp dụng cho một tập dữ liệu, phương pháp tìm kiếm các mối quan hệ giữa các biến trong một nổ lực để giảm đi một số lượng lớn các biến thành các tập hợp nhỏ hơn của các nhân tố tổng hợp (nghĩa là sự kết hợp các biến). Tập hợp cuối cùng của nhân tố tổng hợp là kết quả của việc khám phá các mối quan hệ trong dữ liệu và báo cáo chúng khi tìm thấy (nếu có). Tuy nhiên, trong khi kỹ thuật này là khám phá về bản chất (như tên gọi đã được đề xuất), các nhà nghiên cứu thường có sẵn một nền kiến thức ban đầu để định hướng quyết định của họ liệu có bao nhiêu nhân tố tổng hợp trích xuất từ dữ liệu (Sarstedt và Mooi, 2014). Ngược lại, phân tích nhân tố khẳng định cho phép kiểm định và chứng minh một nhân tố xác định ban đầu và gán các biến quan sát của nó.

Các kỹ thuật thế hệ thứ nhất được áp dụng rộng rãi bởi các nhà nghiên cứu khoa học xã hội. Tuy nhiên, 20 năm qua, ngày càng nhiều nhà nghiên cứu chuyển sang các kỹ thuật thế hệ thứ hai để khắc phục những nhược điểm của phương pháp thế hệ thứ nhất (bảng 1.1). Những phương pháp này, gọi là mô hình cấu trúc tuyến tính (SEM), cho phép các nhà nghiên cứu kết hợp các biến không quan sát được mà những biến này được đo lường gián tiếp bởi các biến quan sát. Ngoài ra, chúng còn tính toán được sai số đo lường trong các biến quan sát (Chin, 1998).

Có hai loại SEM: CB-SEM (Covariance –Based SEM) và PLS-SEM (Partial least squares SEM). CB-SEM chủ yếu được sử dụng để khẳng định (hoặc từ chối) lý thuyết (tức là một tập hợp các mối quan hệ có hệ thống giữa nhiều biến có thể được kiểm tra bằng thực nghiệm). Nó thực hiện bằng cách xác định mô hình lý thuyết đề xuất có thể ước lượng ma trận hiệp phương sai cho một tập hợp dữ liệu mẫu. Ngược lại, PLS-SEM (còn được gọi là mô hình đường dẫn PLS) được sử dụng chủ yếu để phát triển các lý thuyết trong nghiên cứu khám phá. Nó thực hiện việc này bằng cách tập trung giải thích phương sai của các biến phụ thuộc khi kiểm tra mô hình. Chúng tôi sẽ giải thích sự khác biệt này chi tiết hơn nữa trong chương này.

PLS-SEM đang mở ra như một kỹ thuật mô hình thống kê, và trong khi có rất nhiều bài báo được công bố về phương pháp (ví dụ như Chin, 1998; Chin, 2010; Haenlein và Kaplan, 2004; Hair, Ringle, và Sarstedt, 2011; Henseler, Ringle, và Sarstedt, 2012; Henseler, Ringle, và Sinkovics, 2009; Mateos-Aparicio, 2011; Rigdon, 2013; Roldán và Sánchez-Franco, 2012; Tenenhaus và cộng sự, 2005; Wold, 1985) và ứng dụng nó vào nhiều trường hợp khác nhau ( như Valle và Assaker; Hair, Sarstedt, Pieper, và Ringle, 2012; Hair, Sarstedt, Ringle và Mena, 2012; Lee và cộng sự, 2011; Nitzl, 2016; Peng và Lai, 2012; Richter, Sinkovics, Ringle, và Schlãgel; Ringle, Sartedt, và Straub, 2012; Sarstedt, Ringle, Smith, Ream, và Hair, 2014), cho đến ấn bản đầu tiên của quyển sách này, không có một văn bản nào có thể giải thích các khía cạnh cơ bản của phương pháp, đặc biệt là cho người không có nền tảng thống kê có thể hiểu được. Lần tái bản thứ hai của cuốn sách đã mở rộng và làm sáng tỏ bản chất cùng vai trò của PLS-SEM trong nghiên cứu khoa học xã hội và hy vọng các nhà nghiên cứu có được một công cụ cho phép họ theo đuổi các cơ hội nghiên cứu bằng những cách mới và khác biệt.

CÁC CHÚ Ý TRONG VIỆC SỬ DỤNG MÔ HÌNH CẤU TRÚC TUYẾN TÍNH

Tùy thuộc vào câu hỏi nghiên cứu và dữ liệu thực nghiệm sẵn có, các nhà nghiên cứu sẽ phải lựa chọn phương pháp phân tích đa biến phù hợp. Cho dù các nhà nghiên cứu sử dụng phương pháp phân tích đa biến thế hệ thứ nhất hay thứ hai, có một số lưu ý cần thiết trong việc quyết định sử dụng phân tích đa biến, đặc biệt là SEM. Quan trọng nhất là năm yếu tố sau đây: (1) biến tổng hợp, (2) sự đo lường, (3) thang  đo lường, (4) mã hóa, và (5) phân phối dữ liệu.

Các biến tổng hợp

Các biến tổng hợp (hay còn gọi là biến) là sự kết hợp tuyến tính của nhiều biến, được chọn lựa dựa trên các vấn đề nghiên cứu có thể thực hiện được (Hair, Black, Babin, và Anderson, 2010). Quá trình kết hợp các biến liên quan đến việc tính toán một tập các trọng số (giá trị biến), bằng cách nhân trọng số (ví dụ, w1 và w2) với biến quan sát tương ứng (ví dụ, x1 và x2), và tổng hợp chúng.  Công thức toán học cho một kết hợp tuyến tính với năm biến được hiển thị như sau (lưu ý rằng giá trị biến có thể được tính toán cho bất kỳ số lượng các biến):

Giá trị biến tổng hợp: x₁w­₁ + x₂w­₂ + … + x₅w­₅ ,

trong đó x là viết tắt của các biến đơn và w là các trọng số. Tất cả biến x (ví dụ, các câu hỏi trong bảng câu hỏi) có phần trả lời từ nhiều đáp viên có thể được sắp xếp trong một ma trận dữ liệu. Bảng 1.2 trình bày một ma trận dữ liệu, trong đó i là số lượng câu trả lời (ví dụ, số mẫu thu thập). Giá trị biến được tính cho mỗi người được hỏi thứ i trong mẫu.

Bảng 1.2	Ma trận dữ liệu
Trường hợp	x1	x2	...	x5	Giá trị biến
1	x11	x21	...	x51	v1
. . .	. ..	. ..	. ..	. ..	...
i	x1i	x2i	...	x5i	vi

 Đo lường

Đo lường là một khái niệm cơ bản trong nghiên cứu khoa học xã hội. Khi nghĩ về đo lường, điều đầu tiên nghĩ đến thường là một thước đo/quy tắc, mà nó có thể được sử dụng để đo chiều cao hoặc chiều dài của một đồ nội thất. Nhưng có rất nhiều ví dụ khác về đo lường trong cuộc sống. Khi lái xe, bạn sử dụng công tơ mét để đo tốc độ chiếc xe, máy đo nhiệt để đo nhiệt độ của động cơ, và đồng hồ để xác định còn bao nhiêu nhiên liệu trong xe của bạn. Nếu bạn bị bệnh, bạn sử dụng nhiệt kế để đo nhiệt độ, và khi ăn kiêng, bạn đo cân nặng của mình trên cân sức khỏe.

Đo lường là quá trình gán các số cho một biến dựa trên một tập hợp các quy tắc (Hair, Wolfinbarger Celsi, Money, Samouel, và Page, 2016). Các quy tắc này được sử dụng để gán các con số đại diện chính xác cho các biến. Với một số biến, các quy tắc rất dễ làm theo, trong khi với các biến khác, các quy tắc gặp nhiều khó khăn để áp dụng. Ví dụ, nếu biến đó là giới tính, thì rất dễ dàng để gán 1 cho nữ giới và 0 cho nam giới. Tương tự như vậy, nếu biến đó là tuổi hoặc chiều cao thì cũng dễ dàng để gán số. Nhưng nếu biến đó là sự hài lòng hoặc tin tưởng? Đo lường trong những tình huống này khó khăn hơn vì hiện tượng trên rất trừu tượng, phức tạp và không trực tiếp quan sát được. Do đó chúng ta sẽ nói về sự đo lường các biến tiềm ẩn (tức là không quan sát được) hoặc các khái niệm nghiên cứu.

Chúng ta không thể đo lường trực tiếp các khái niệm trừu tượng như sự hài lòng hoặc sự tin tưởng. Tuy nhiên, chúng ta có thể đo lường các biến chỉ báo (indicators) hoặc biến quan sát mà chúng ta đã thống nhất gọi là sự hài lòng hoặc tin tưởng, ví dụ, về mặt thương hiệu, sản phẩm, hoặc công ty. Cụ thể, khi các khái niệm khó đo lường, có một cách tiếp cận là đo lường chúng gián tiếp với một tập hợp các biến chỉ báo được dùng như là các biến đại diện (proxy variables). Mỗi biến quan sát đại diện cho một khía cạnh riêng biệt của một khái niệm trừu tượng lớn hơn. Ví dụ, nếu khái niệm này là sự hài lòng đối với nhà hàng, thì một số biến đại diện có thể được sử dụng để đo lường khái niệm này như sau:

1.     Mùi vị của thực phẩm rất tuyệt vời.

2.      Sự phục vụ nhanh chóng đáp ứng được mong đợi của tôi.

3.     Nhân viên phục vụ rất am hiểu về các món ăn trong thực đơn.

4.      Nhạc nền trong nhà hàng dễ chịu.

5.     Chất lượng bữa ăn tương xứng so với giá.

Bằng cách kết hợp một số biến đo lường để tạo thành một thang đo (hoặc chỉ số - Index), chúng ta có

 thể gián tiếp đo lường khái niệm tổng thể của sự hài lòng về nhà hàng. Thông thường, các nhà nghiên 

cứu sử dụng một số biến đo lường để tạo thành một thang đo đa biến, gián tiếp đo lường một khái niệm,

 như sự hài lòng về nhà hàng của ví dụ trên. Một số biện pháp đo lường được kết hợp để tạo thành một

 điểm tổng duy nhất (tức là điểm số của biến). Trong một số trường hợp, điểm số tổng là một tổng hợp 

đơn giản của một số biện pháp đo lường. Trong trường hợp khác, điểm số của các đo lường riêng lẻ 

được kết hợp để tạo thành một điểm tổng, sử dụng quá trình tuyến tính trọng số cho các đo lường riêng 

lẻ. Logic của việc sử dụng các biến số riêng lẻ để đo lường một khái niệm trừu tượng như là sự hài lòng

 về nhà hàng sẽ được chính xác hơn. Độ chính xác mang tính dự đoán được cải thiện dựa trên giả định

việc sử dụng một số biến quan sát để đo lường một khái niệm đơn lẻ có nhiều khả năng đại diện được 

cho tất cả các khía cạnh khác nhau của khái niệm. Điều này liên quan đến việc giảm sai số đo lường,

 đó là sự khác biệt giữa giá trị thực sự của một biến và giá trị thu được bởi một phép đo. 

Có rất nhiều nguyên nhân dẫn đến sai số đo lường, bao gồm các câu hỏi tối nghĩa trong một cuộc khảo

 sát, hiểu sai về cách tiếp cận thang đo, và ứng dụng không chính xác phương pháp thống kê. 

Thật vậy, tất cả các phép đo sử dụng trong phân tích đa biến có khả năng chứa một vài sai số đo lường.

 Do đó, mục tiêu là giảm sai số đo lường càng nhiều càng tốt. Thay vì sử dụng nhiều biến quan sát, các

 nhà nghiên cứu đôi khi lựa chọn việc sử dụng các biến đơn để đo lường các khái niệm như sự hài lòng

 hoặc ý định mua. Ví dụ, chúng ta có thể chỉ sử dụng “Nhìn chung, tôi hài lòng với nhà hàng này” để đo

 lường sự hài lòng về nhà hàng thay vì sử dụng tất cả 5 biến được mô tả ở trên. Đây là một cách tốt để 

làm cho bảng câu hỏi ngắn hơn, nhưng nó cũng làm giảm chất lượng đo lường. Chúng ta sẽ thảo luận 

về các nguyên tắc cơ bản của đo lường và đánh giá đo lường trong các bài tiếp theo.

Các Thang đo

Thang đo là một công cụ với một số câu hỏi đóng đã xác định trước, được sử dụng để có được một câu trả lời cho mỗi câu hỏi. Có bốn loại thang đo, mỗi loại đại diện cho một mức độ đo lường khác nhau gồm: định danh, thứ bậc, khoảng cách, và tỷ lệ. Thang đo định danh là mức thấp nhất của thang đo bởi vì chúng có nhiều hạn chế nhất về các loại phân tích có thể được thực hiện. Một thang đo định danh gán số có thể được sử dụng để xác định và phân loại các đối tượng (ví dụ, con người, công ty, sản phẩm,...) và cũng được gọi là một thang đo phân loại. Ví dụ, nếu một cuộc khảo sát để xác định nghề nghiệp của ông ấy hoặc cô ấy là bác sĩ, luật sư, giáo viên hay kỹ sư,..., thì câu hỏi có thang đo định danh. Thang đo định danh có thể có hai hoặc nhiều phân loại, nhưng mỗi loại phải được loại trừ lẫn nhau, và tất cả các thể loại phải được tính đến. Một con số có thể được gán vào để xác định mỗi thể loại, và những con số có thể được sử dụng để đếm số lượng các trả lời trong mỗi thể loại, hoặc tỷ lệ phần trăm của mỗi loại.

Cấp độ cao hơn của thang đo được gọi là thứ bậc. Nếu chúng ta có một biến được đo dựa trên một thang đo thứ bậc chúng ta sẽ biết rằng giá trị của biến đó tăng hoặc giảm, điều này cung cấp những thông tin có ý nghĩa. Ví dụ, nếu chúng ta mã hóa việc sử dụng sản phẩm của khách hàng là: người không sử dụng = 0, người sử dụng ít = 1, và người sử dụng nhiều = 2, chúng ta biết rằng nếu giá trị của các biến về việc sử dụng tang lên, mức độ sử dụng cũng tăng lên. Do đó, đo lường trên một thang đo thứ bậc sẽ cung cấp thông tin về thứ tự trong các quan sát của chúng ta. Tuy nhiên, không thể giả định rằng sự khác biệt theo thứ bậc có khoảng cách như nhau. Đó là, chúng ta không biết rằng sự khác biệt giữa “người không sử dụng” và “người sử dụng ít” có tương tự như giữa “người sử dụng ít” và “người sử dụng nhiều” hay không, mặc dù sự khác biệt trong các giá trị (tức là, 0-1 và 1- 2) là bằng nhau. Do đó, không thích hợp để tính toán trung bình hoặc phương sai cho các dữ liệu thứ bậc.

Nếu cái gì đó được đo bằng thang đo khoảng, chúng ta có thông tin chính xác về thứ tự xếp hạng của chúng, hơn nữa, chúng ta có thể giải thích tầm quan trọng của sự khác biệt về giá trị một cách trực tiếp. Ví dụ, nếu nhiệt độ là 80°F, chúng ta biết rằng nếu nó giảm xuống đến 75°F, sự khác biệt chính xác là 5°F. Sự khác biệt 5°F này cũng giống như sự gia tăng từ 80°F đến 85°F. “Khoảng cách” chính xác này được gọi là khoảng cách đều nhau và tỷ lệ khoảng cách đều rất cần thiết cho những kỹ thuật phân tích nhất định, chẳng hạn như SEM. Thang đo khoảng không có một điểm 0 tuyệt đối. Nếu nhiệt độ là 0°F, trời có thể lạnh, nhưng nhiệt độ có thể giảm hơn nữa. Giá trị 0 do đó không có nghĩa là không có nhiệt độ (Sarstedt và Mooi, 2014). Giá trị của thang đo khoảng thì hầu như bất kỳ loại tính toán nào cũng có thể được thực hiện, bao gồm cả giá trị trung bình và độ lệch chuẩn. Hơn nữa, có thể chuyển đổi và mở rộng thang đo khoảng này thành thang đo khoảng khác. Ví dụ, thay vì °F, nhiều quốc gia có thể sử dụng °C để đo nhiệt độ. Trong khi 0°C đánh dấu điểm đóng băng, 100°C mô tả điểm sôi của nước. Ta có thể chuyển đổi nhiệt độ từ °F thành °C bằng cách sử dụng công thức sau: °C= (°F-32) * 5/9. Theo cách tương tự, có thể chuyển đổi dữ liệu (thông qua việc thay đổi tỷ lệ) của một thang đo từ 1 đến 5 thành dữ liệu của thang đo từ 0 đến 100: [(điểm dữ liệu của thang đo từ 1 đến 5) -1] / 4 * 100

Thang đo tỷ lệ cung cấp thông tin nhiều nhất. Nếu một điều gì đó được đo bằng thang đo tỷ lệ, chúng ta biết rằng giá trị 0 có ý nghĩa, nó là một đặc tính cụ thể cho một biến không hiện diện. Ví dụ, nếu một khách hàng mua không sản phẩm (giá trị = 0), thì anh ta, cô ta thực sự không mua sản phẩm. Hoặc, nếu chúng ta không chi tiền vào quảng cáo cho một sản phẩm mới (giá trị = 0), thì chúng ta thực sự không chi tiền. Do đó, điểm không hay gốc của biến là bằng 0. Các đo lường về chiều dài, khối lượng, âm lượng hay thời gian đều sử dụng thang đo tỷ lệ. Với thang đo tỷ lệ, tất cả các tính toán số học đều có thể thực hiện được.

Mã hoá

Việc gán số cho biến đo lường để phân loại được gọi là mã hóa (coding). Trong nghiên cứu khảo sát, dữ liệu thường được tiền mã hoá (precoding). Tiền mã hoá là gán các số trước lần trả lời (ví dụ, điểm thang đo) được chỉ định trên bảng câu hỏi. Chẳng hạn như, thang đo đồng ý - không đồng ý 10 điểm thường sẽ gán số 10 là điểm cuối cao nhất “đồng ý” và 1 là điểm cuối thấp nhất “không đồng ý”, các điểm giữa sẽ được mã hóa từ 2 đến 9. Hậu mã hoá (postcoding) là gán số để phân loại cho các câu trả lời sau khi dữ liệu được thu thập. Phần trả lời có thể là câu hỏi mở hoặc đóng được dùng trong khảo sát định lượng hoặc một cuộc phỏng vấn trong nghiên cứu định tính.

Mã hóa rất quan trọng trong ứng dụng phân tích đa biến vì nó quyết định khi nào và dạng thang đo nào có thể được sử dụng. Ví dụ, các biến đo bằng thang đo khoảng và tỷ lệ luôn luôn có thể được sử dụng với phân tích đa biến. Tuy nhiên, khi sử dụng thang đo thứ bậc như thang đo Likert (phổ biến trong SEM), các nhà nghiên cứu phải đặc biệt chú ý đến mã hóa để đáp ứng yêu cầu của khoảng cách đều nhau. Ví dụ, khi sử dụng thang đo Likert 5-điểm với các hạng mức:  (1) hoàn toàn không đồng ý, (2) không đồng ý, (3) vừa đồng ý vừa không đồng ý, (4) đồng ý, và (5) hoàn toàn đồng ý, hàm ý là “khoảng cách” giữa mức 1 và 2 cũng giống như giữa mức 3 và 4. Ngược lại, cùng một thang đo Likert nhưng sử dụng các mức độ: (1) không đồng ý, (2) vừa đồng ý vừa không đồng ý, (3) phần nào đồng ý , (4) đồng ý, và (5) hoàn toàn đồng ý là khoảng cách không đều nhau, vì chỉ có một mức độ có thể nhận được tỷ lệ dưới mức trung tính “vừa đồng ý vừa không đồng ý.” Điều này sẽ tạo nên sự thiên lệch cho các kết quả đầu ra. Một thang đo Likert tốt như ở trên, sẽ trình bày đối xứng qua mức trung gian, đã được xác định rõ ràng cho mỗi mức độ. Như trong thang đo đối xứng, khoảng cách đều nhau sẽ được quan sát rõ ràng hơn hoặc, ít nhất là suy ra. Khi một thang đo Likert được coi là đối xứng và cách đều, thì nó sẽ hoạt động giống như một thang đo khoảng. Vì vậy, trong khi thang đo Likert là thứ bậc, nếu được trình bày tốt nó có khả năng tương tự với cấp độ đo lường khoảng, và các biến tương ứng có thể được sử dụng trong SEM.

Phân phối dữ liệu

Khi các nhà nghiên cứu thu thập dữ liệu định lượng, các câu trả lời cho những câu hỏi được báo cáo dưới dạng phân phối dựa trên các câu trả lời có sẵn (đã được xác định trước). Ví dụ, nếu câu trả lời được yêu cầu sử dụng theo thang đo đồng ý – không đồng ý 9 - điểm, phân phối các câu trả lời tương ứng với các mức có sẵn (1, 2, 3,…, 9) có thể được tính toán và trình bày trong bảng hoặc biểu đồ. Bảng 1.3 đưa ra một ví dụ về các tần số của một biến x tương ứng.

Có thể thấy, hầu hết các phản hồi chỉ ra mức điểm 5 trên thang 9-điểm, tiếp theo là điểm 4 và 6, tiếp đến 3 và 7, và vân vân. Nhìn chung, các tần số xuất hiện theo dạng hình chuông, đường cong đối xứng xung quanh giá trị trung bình là 5. Đường cong hình chuông này là phân phối chuẩn mà nhiều kỹ thuật phân tích yêu cầu để cho ra kết quả chính xác.

Trong khi nhiều dạng phân phối khác nhau đang tồn tại (ví dụ, phân phối chuẩn, nhị thức, Poisson), các nhà nghiên cứu làm việc với SEM thường chỉ cần phân biệt phân phối chuẩn và phân phối không chuẩn. Phân phối chuẩn thường phù hợp, đặc biệt là khi làm việc với CB-SEM. Ngược lại, PLS-SEM thường không có giả định về sự phân phối dữ liệu. Tuy nhiên, vì những lý do được thảo luận trong chương sau, việc xem xét phân phối vẫn rất cần thiết khi làm việc với PLS-SEM. Để đánh giá xem dữ liệu có phân phối chuẩn hay không, các nhà nghiên cứu có thể xem lại các kiểm định thống kê chẳng hạn như kiểm định Kolmogorov-Smirnov và kiểm định Shapiro-Wilk (Sarstedt và Mooi, 2014). Ngoài ra, các nhà nghiên cứu có thể kiểm tra hai đo lường của phân bố - độ lệch và độ nhọn (Chương 2) - cho phép đánh giá mức độ lệch của dữ liệu so với trạng thái phân phối chuẩn (Hair và cộng sự, 2010).

MÔ HÌNH CẤU TRÚC TUYẾN TÍNH VỚI MÔ HÌNH ĐƯỜNG DẪN BÌNH PHƯƠNG TỐI THIỂU TỪNG PHẦN (PLS-SEM)

Mô hình đường dẫn với các biến tiềm ẩn

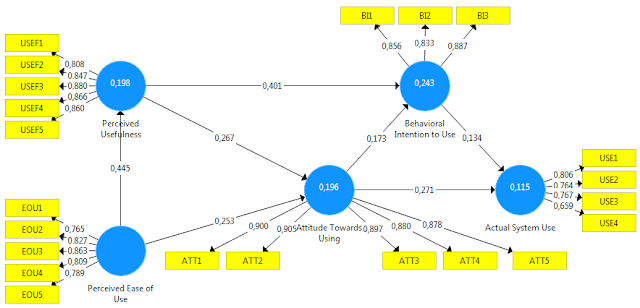
Mô hình đường dẫn là các biểu đồ hiển thị trực quan các mối quan hệ của giả thuyết và biến, được kiểm tra khi áp dụng SEM (Hair và cộng sự, 2011; Hair, Celsi, Money, Samouel, và Page, 2016). Ví dụ về mô hình đường dẫn sẽ được trình bày ở bảng 1.4.

Khái niệm nghiên cứu (construct) (tức là các biến không được đo lường một cách trực tiếp) được thể hiện trong mô hình đường dẫn bằng các hình tròn hoặc hình bầu dục (Y₁ đến Y₄). Các biến chỉ báo (Indicator), cũng được gọi là các biến đo lường (Item) hoặc các biến quan sát (Manifest variable), là những biến đại diện (Proxy variable) được đo lường trực tiếp, chứa dữ liệu thô. Nó được trình bày trong mô hình đường dẫn bởi các hình chữ nhật (x₁ đến x₁₀). Các mối quan hệ giữa các khái niệm nghiên cứu cũng như giữa các khái niệm nghiên cứu và các biến chỉ báo của chúng được thể hiện bằng các mũi tên. Trong PLS-SEM, những mũi tên luôn là một chiều, đại diện cho mối quan hệ trực tiếp. Những mũi tên một chiều được xem như là những mối quan hệ dự báo, với sự hỗ trợ mạnh mẽ của lý thuyết, nó có thể được hiểu là những mối quan hệ nhân quả.

        Mô hình đường dẫn PLS bao gồm hai yếu tố. Đầu tiên, đó là Mô hình cấu trúc (Structural model) (còn gọi là mô hình nội tại trong PLS-SEM) trình bày các khái niệm nghiên cứu (vòng tròn hoặc hình bầu dục). Mô hình cấu trúc cũng hiển thị các mối quan hệ (đường dẫn) giữa các khái niệm nghiên cứu. Thứ hai, đó là Mô hình đo lường (Measurement model) (còn gọi là mô hình bên ngoài trong PLS-SEM) của các khái niệm nghiên cứu, hiển thị các mối quan hệ giữa các khái niệm nghiên cứu và các biến quan sát (hình chữ nhật). Trong hình 1.4 có hai loại mô hình đo lường: một là các biến tiềm ẩn ngoại sinh - exogenous latent variable (là những khái niệm nghiên cứu mà nó giải thích cho những khái niệm nghiên cứu khác trong mô hình) và một là các biến tiềm ẩn nội sinh - endogenous latent variable (là những khái niệm nghiên cứu đang được giải thích trong mô hình). Thay vì đề cập đến mô hình đo lường của các biến tiềm ẩn ngoại sinh và nội sinh, các nhà nghiên cứu thường xuyên tham khảo mô hình đo lường của một biến tiềm ẩn cụ thể. Ví dụ, x­­₁ tới  x₃ là các biến quan sát được sử dụng trong mô hình đo lường của Y₁ trong khi Y₄ chỉ có biến quan sát x₁₀ trong mô hình đo lường.

Phần sai số (Error term) (ví dụ, e₇ hoặc e₈ hình 1.4) được kết nối với khái niệm (nội sinh) và biến đo lường (kết quả) bằng những mũi tên một chiều. Phần sai số đại diện cho phương sai không giải thích được khi mô hình đường dẫn được ước lượng. Trong hình 1.4, các sai số e₇ đến e₉ nằm trên những biến quan sát mà mối quan hệ của nó đi từ khái niệm nghiên cứu đến các biến quan sát (tức là biến quan sát đo lường kết quả). Ngược lại, các biến đo lường nguyên nhân x₁ tới x₆, mối quan hệ đi từ các biến quan sát đến khái niệm nghiên cứu, không có phần sai số. Cuối cùng, đối với khái niệm đơn biến Y₄, hướng của các mối quan hệ giữa khái niệm và biến quan sát không quan trọng bằng khái niệm và biến quan sát tương đương. Vì lí do đó, không có phần sai số kết nối với x₁₀. Mô hình cấu trúc cũng chứa phần sai số. Trong hình 1.4, z₃ và z₄ có liên quan đến biến tiềm ẩn nội sinh Y₃ và Y₄ (lưu ý rằng các sai số trên các khái niệm nghiên cứu và các biến đo lường được dán nhãn khác nhau). Ngược lại, các biến tiềm ẩn ngoại sinh chỉ giải thích cho các biến tiềm ẩn khác trong mô hình cấu trúc không có phần sai số.

Mô hình đường dẫn được xây dựng dựa trên lý thuyết. Lý thuyết (Theory) là một tập hợp các giả thuyết liên quan một cách hệ thống được phát triển theo phương pháp khoa học, có thể được sử dụng để giải thích và dự báo kết quả. Như vậy, giả thuyết là phỏng đoán mang tính cá nhân, trong khi lý thuyết gồm nhiều giả thuyết liên kết với nhau một cách hợp lý và có thể được kiểm tra bằng thực nghiệm. Hai loại lý thuyết cần để xây dựng mô hình đường dẫn là: Lý thuyết đo lường và lý thuyết cấu trúc. Lý thuyết cấu trúc xác định cách thức các khái niệm nghiên cứu thể hiện mối liên quan đến nhau trong mô hình cấu trúc, trong khi lý thuyết đo lường quy định cụ thể cách mỗi khái niệm nghiên cứu được đo lường.

Lý thuyết đo lường

Lý thuyết đo lường chỉ rõ cách các biến tiềm ẩn (các khái niệm nghiên cứu) được đo. Nói chung, có hai cách khác nhau để đo lường các biến không quan sát được. Một cách được gọi là đo lường kết quả (reflective measurement) và cách còn lại được gọi là đo lường nguyên nhân (formative measurement). Khái niệm nghiên cứu Y₁ và Y₂ trong hình 1.4 được mô phỏng dựa trên mô hình đo lường nguyên nhân (formative measurement model). Lưu ý rằng các mũi tên chỉ hướng đi từ các biến quan sát tới khái niệm nghiên cứu (x_1, x_2, x₃ đến Y₁ và x_4, x_5, x₆ đến Y₂), chỉ ra (dự báo) mối quan hệ nhân quả theo hướng đó.

Ngược lại, Y₃ trong hình được mô phỏng dựa trên mô hình đo lường kết quả (reflective measurement model). Với các biến quan sát kết quả, hướng của các mũi tên đi từ khái niệm nghiên cứu đến các biến quan sát, chỉ ra giả định rằng khái niệm nghiên cứu đã dẫn đến sự đo lường (chính xác hơn là sự đồng thay đổi) của biến quan sát. Như đã trình bày trong hình 1.4, đo lường kết quả có một phần sai số được kết hợp với mỗi biến quan sát, trong khi điều này không xảy ra với đo lường nguyên nhân.  Đo lường nguyên nhân được giả định là không có sai số (error free) (Diamantopoulos, 2011). Cuối cùng, lưu ý rằng Y₄ được đo lường chỉ bằng một biến quan sát đơn chứ không phải là đo lường đa biến. Vì thế, mối quan hệ giữa khái niệm nghiên cứu và biến quan sát là không được định hướng.

Cách tiếp cận mô hình hóa các khái niệm nghiên cứu ( nguyên nhân hay kết quả, đa biến hay đơn biến) là một yếu tố quan trọng trong việc phát triển mô hình đường dẫn. Những cách tiếp cận nhằm mô hình hóa khái niệm nghiên cứu được giải thích chi tiết hơn trong Chương 2.

Lý thuyết cấu trúc

Lý thuyết cấu trúc cho thấy cách các biến tiềm ẩn liên quan đến nhau (tức là, nó cho thấy các khái niệm nghiên cứu và mối quan hệ đường dẫn giữa chúng trong mô hình cấu trúc). Các vị trí và thứ tự của các khái niệm nghiên cứu được xác định dựa trên lý thuyết hay kinh nghiệm và kiến thức tích lũy của nhà nghiên cứu. Khi các mô hình đường dẫn được phát triển, trình tự là từ trái sang phải. Các biến ở phía bên trái của mô hình đường dẫn là các biến độc lập, và biến bất kỳ ở phía bên phải là biến phụ thuộc. Hơn nữa, các biến bên trái sẽ hiển thị trước và dự đoán các biến bên phải. Tuy nhiên, các biến cũng có thể đóng vai trò là cả biến độc lập và phụ thuộc.

Khi các biến tiềm ẩn được dùng như là các biến độc lập, chúng được gọi là các biến tiềm ẩn ngoại sinh (Y₁ và Y₂). Khi các biến tiềm ẩn được dùng như là các biến phụ thuộc (Y4) hoặc là cả biến độc lập và phụ thuộc (Y₃), chúng được gọi là các biến tiềm ẩn nội sinh. Bất kỳ biến tiềm ẩn nào mà chỉ có những mũi tên một chiều đi ra khỏi nó là một biến tiềm ẩn ngoại sinh. Ngược lại, các biến tiềm ẩn nội sinh có thể có mũi tên một chiều đi vào và ra khỏi chúng (Y₃) hoặc chỉ đi vào chúng (Y₄). Lưu ý rằng các biến tiềm ẩn ngoại sinh Y₁ và Y₂ không có phần sai số bởi vì các khái niệm nghiên cứu là những thực thể (biến độc lập) giải thích cho biến phụ thuộc trong mô hình đường dẫn.

PLS-SEM, CB-SEM VÀ HỒI QUY DỰA TRÊN CÁC ĐIỂM TỔNG

    Có hai phương pháp chính để ước lượng các mối quan hệ trong một mô hình cấu trúc tuyến tính (Hair và cộng sự, 2010;. Hair và cộng sự, 2014). Một là phương pháp được áp dụng rộng rãi CB-SEM. Hai là PLS-SEM, trọng tâm của cuốn sách này. Mỗi phương pháp thích hợp cho một bối cảnh nghiên cứu khác nhau, và các nhà nghiên cứu cần phải hiểu sự khác nhau để áp dụng đúng phương pháp. Cuối cùng, một số nhà nghiên cứu đã lập luận về việc sử dụng các hồi quy dựa trên điểm tổng, thay vì một vài trọng số biến quan sát được thực hiện bởi PLS-SEM. Cách tiếp cận này thực tế không có giá trị ngoài PLS-SEM. Vì lý do đó, chúng tôi chỉ thảo luận điểm tổng một đoạn ngắn và tập trung vào phương pháp PLS-SEM và CB-SEM.

Để trả lời các câu hỏi khi nào thì sử dụng PLS-SEM hoặc CB-SEM, các nhà nghiên cứu nên tập trung vào các đặc điểm và mục tiêu giúp phân biệt hai phương pháp (Hair, Sarstedt, Ringle và cộng sự, 2012). Trong những trường hợp lý thuyết chưa phát triển, các nhà nghiên cứu nên cân nhắc việc sử dụng các PLS-SEM như một cách tiếp cận thay thế cho CB-SEM. Điều này đặc biệt đúng nếu mục tiêu chính của việc áp dụng mô hình cấu trúc là dự báo và giải thích về khái niệm nghiên cứu mục tiêu (Rigdon, 2012).

Sự khác biệt về mặt khái niệm quan trọng giữa PLS-SEM và CB-SEM liên quan đến cách thức mỗi phương pháp xử lý các biến tiềm ẩn trong mô hình. CB-SEM xem xét các khái niệm nghiên cứu như là các yếu tố chung giải thích sự đồng biến đổi (covariation) giữa các biến quan sát liên quan của nó. Điểm số của những yếu tố chung này không được biết đến và cũng không cần thiết trong việc ước lượng các tham số mô hình. Mặt khác, PLS-SEM sử dụng các đại diện để biểu diễn các khái niệm nghiên cứu quan tâm, là trọng số hợp nhất của các biến quan sát cho một khái niệm nghiên cứu cụ thể. Vì lý do này, PLS-SEM hình thành một cách tiếp cận dựa trên sự tổng hợp đến SEM, làm dịu các giả định mạnh mẽ của CB-SEM rằng tất cả sự biến thiên đồng thời giữa một tập hợp các biến quan sát được giải thích bằng các yếu tố chung (Henseler và cộng sự. 2014; Rigdon, 2012; Rigdon và cộng sự, 2014). Đồng thời, sử dụng các trọng số hợp nhất của các biến quan sát để giải thích các sai số đo lường, do đó làm cho PLS-SEM vượt trội hơn so với hồi quy sử dụng điểm tổng nhiều lần. Trong trường hợp hồi quy điểm tổng, nhà nghiên cứu giả định rằng các biến quan sát đều có trọng số bằng nhau, có nghĩa là mỗi biến quan sát đóng góp như nhau để tạo thành tổng hợp (Henseler và cộng sự, 2014). Xem lại mô tả của chúng ta về các biến tổng ngay từ đầu của chương này, điều này ngụ ý rằng tất cả các trọng số w sẽ được đặt thành 1. Công thức toán học cho sự kết hợp tuyến tính với 5 biến quan sát như sau:

Giá trị tổng = 1.x₁ +1.x₂ +1.x₃ +1.x₄ +1.x₅

Ví dụ, nếu đáp viên cho điểm 4, 5, 4, 6 và 7 cho 5 biến, giá trị tổng tương ứng sẽ là 26. Trong khi việc áp dụng khá dễ dàng, hồi quy bằng cách sử dụng điểm tổng đã làm cân bằng bất kỳ sự khác biệt trong các trọng số biến riêng lẻ. Tuy nhiên, những khác biệt này lại rất phổ biến trong thực tế khi làm nghiên cứu, và đòi hỏi phải bỏ qua những sai lệch đáng kể trong ước lượng tham số (ví dụ Thiele, Sarstedt, và Ringle, 2015). Hơn nữa, tìm hiểu về trọng số của từng biến riêng lẻ cung cấp những hiểu biết rất quan trọng như khi nhà nghiên cứu tìm hiểu về tầm quan trọng của mỗi biến đo lường để tạo thành một tổng hợp, trong một ngữ cảnh nhất định (ví dụ mối quan hệ của nó với các biến hỗn hợp khác trong mô hình cấu trúc). Ví dụ như khi đo lường mức độ hài lòng của khách hàng, nhà nghiên cứu sẽ biết được khía cạnh bao gồm những biến quan sát cụ thể nào sẽ có ý nghĩa đặc biệt đối với việc tạo ra sự hài lòng.

Lưu ý quan trọng là các đại diện được tạo ra bởi PLS-SEM không được giả định giống nhau với các khái niệm nghiên cứu mà chúng thay thế. Chúng được công nhận như là một cách tính gần đúng (Rigdon, 2012). Kết quả là, một số học giả xem CB-SEM như là một phương pháp trực tiếp và chính xác hơn để đo lường thực nghiệm các khái niệm lý thuyết, trong khi PLS-SEM cung cấp các phép tính xấp xỉ, gần đúng. Tuy nhiên, các học giả khác lại cho rằng quan điểm như vậy khá là thiển cận vì các yếu tố chung trong CB-SEM cũng không hẳn là tương đương với các khái niệm lý thuyết, trọng tâm của nghiên cứu. Trên thực tế, luôn tồn tại một khoảng cách lớn về giá trị giữa khái niệm mà nhà nghiên cứu dự định đo lường và khái niệm được sử dụng để đo lường khái niệm cụ thể đó.

Trong nghiên cứu khoa học xã hội, xem đo lường như một phép tính xấp xỉ dường như thực tế hơn, làm cho sự phân biệt giữa PLS-SEM và CB-SEM về việc xử lý các khái niệm trở nên có vấn đề. Quan điểm này cũng được hỗ trợ bởi cách CB-SEM được áp dụng trong thực tiễn nghiên cứu. Khi sử dụng CB-SEM, các mô hình giả thuyết ban đầu gần như luôn luôn thể hiện sự phù hợp không đầy đủ. Trong phần thảo luận, các nhà nghiên cứu nên từ chối mô hình và xem xét lại nghiên cứu (thường đòi hỏi thu thập dữ liệu mới), đặc biệt khi nhiều biến phải bị xóa đi để đạt được sự phù hợp (Hair và cộng sự, 2010). Ngoài ra, thường xuyên nhắc lại mô hình lý thuyết phát triển ban đầu nhằm nỗ lực cải thiện các chỉ số phù hợp vượt quá ngưỡng đề xuất. Bằng cách làm như vậy, các nhà nghiên cứu đạt được một mô hình với sự phù hợp có thể chấp nhận, và họ kết luận là chấp nhận lý thuyết. Thật không may, lý thuyết được hỗ trợ này gần như không bao giờ áp dụng được trong thực tế. Thay vào đó, các nhà nghiên cứu phải tham gia vào các nghiên cứu thăm dò khám phá, trong đó các tập con mô hình được sửa đổi với mục đích đạt đến một mô hình thỏa đáng. Tuy nhiên, các mô hình là sản phẩm của sự sửa đổi như vậy thường không tương ứng tốt với các mô hình thực sự và có xu hướng đơn giản hoá (Sarstedt, Ringle, Henseler, và Hair, 2014).

Ngoài những khác biệt trong triết lý đo lường, cách xử lý khác nhau của các biến tiềm ẩn, và cụ thể hơn, sự có sẵn của các điểm biến tiềm ẩn cũng có những hậu quả đối với các lĩnh vực áp dụng của phương pháp. Cụ thể, mặc dù có thể ước tính các điểm biến tiềm ẩn trong khuôn khổ CB-SEM, nhưng các điểm số ước tính này không phải là duy nhất. Đó là, một số vô hạn của các tập hợp điểm biến tiềm ẩn khác nhau, phù hợp với mô hình nhất có thể. Một hệ quả quan trọng của yếu tố (điểm) không xác định này là sự tương quan giữa một yếu tố chung và bất kỳ biến nào bên ngoài mô hình nhân tố là không xác định. Đó là, chúng có thể là cao hoặc thấp, tùy thuộc vào tập hợp các điểm số nhân tố nào được chọn. Kết quả là, hạn chế này làm cho CB-SEM cực kỳ không phù hợp để dự báo. Trái lại, một ưu điểm chính của PLS-SEM là nó luôn luôn tạo ra một điểm số cụ thể (nghĩa là, xác định) cho từng tổng hợp của từng quan sát, ngay khi các trọng số được thiết lập. Những điểm số xác định này đại diện cho khái niệm được đo, cũng giống như các yếu tố là đại diện cho biến khái niệm trong CB-SEM (Becker, Rai, và Rigdon, 2013). Sử dụng các đại diện này như đầu vào, PLS-SEM áp dụng hồi quy bình phương tối thiểu (OLS) với mục tiêu làm giảm thiểu các sai số (tức là phương sai phần dư) của các biến nội sinh. Nói cách khác, PLS-SEM ước lượng các hệ số (tức là các mối quan hệ mô hình đường dẫn) để tối đa hóa giá trị R² của khái niệm nội sinh (mục tiêu). Tính năng này đạt được mục tiêu dự báo của PLS-SEM. Do đó PLS-SEM là phương pháp được ưa thích khi mục tiêu nghiên cứu là phát triển lý thuyết và giải thích phương sai (dự báo khái niệm nghiên cứu). Vì lý do này, PLS-SEM được coi là phương pháp SEM dựa vào phương sai

Lưu ý rằng PLS-SEM là tương tự nhưng không tương đương với hồi quy PLS - một kỹ thuật phân tích dữ liệu đa biến phổ biến khác. Hồi quy PLS là một phương pháp hồi quy dựa trên việc khám phá các mối quan hệ tuyến tính giữa nhiều biến độc lập với một hoặc nhiều biến phụ thuộc. Hồi quy PLS khác với hồi quy thông thường, tuy nhiên, vì trong việc phát triển các mô hình hồi quy, nó xây dựng các yếu tố tổng hợp từ cả nhiều biến độc lập và nhiều biến phụ thuộc bằng cách phân tích thành phần chính. Mặt khác, PLS-SEM dựa trên mối quan hệ liên kết giữa các khái niệm nghiên cứu, cũng như giữa các khái niệm nghiên cứu và các biện pháp đo lường của nó (xem thêm Mateos-Aparicio, 2011) để thấy sự so sánh chi tiết hơn giữa PLS-SEM và hồi quy PLS).

Một số cân nhắc quan trọng khi quyết định có hay không áp dụng PLS-SEM. Những cân nhắc này cũng có nguồn gốc từ đặc điểm của phương pháp. Các tính chất thống kê của các thuật toán PLS-SEM có các tính năng quan trọng liên quan đến các đặc tính của dữ liệu và mô hình sử dụng. Hơn nữa, các tính chất của các phương pháp PLS-SEM cũng ảnh hưởng đến việc đánh giá các kết quả. Có 4 vấn đề quan trọng liên quan đến việc áp dụng các PLS-SEM (Hair và cộng sự, 2011; Hair, Sarstedt, Ringle và cộng sự, 2012): (1) dữ liệu, (2) đặc tính mô hình, (3)  thuật toán PLS-SEM, và (4) các vấn đề đánh giá mô hình. Hình 1.5 tóm tắt các đặc điểm chính của PLS-SEM. Cái nhìn tổng quan ban đầu của những vấn đề này được quy định trong chương 1, và lời giải thích chi tiết hơn được cung cấp trong phần sau của cuốn sách, đặc biệt là khi chúng liên quan đến các thuật toán PLS-SEM và đánh giá kết quả.

PLS-SEM hoạt động hiệu quả với cỡ mẫu nhỏ và các mô hình phức tạp và không cần giả định về dữ liệu cơ bản (Cassel, Hackyl, và Westlund, 1999). Ví dụ, khác với CB-SEM dựa trên khả năng sự phù hợp cực đại (maximum likelihood), CB - SEM đòi hỏi dữ liệu phân phối chuẩn và hồi quy bằng cách sử dụng các điểm tổng, giả định các phần dư có phân phối chuẩn, thì PLS-SEM không đưa ra các giả định về phân phối (nghĩa là nó là phi tham số). Ngoài ra, PLS-SEM có thể dễ dàng xử lý các mô hình đo lường nguyên nhân và kết quả, cũng như khái niệm đơn biến, không có các vấn đề nhận dạng (identification). Do đó, nó có thể được áp dụng trong một loạt các tình huống nghiên cứu. Khi áp dụng PLS - SEM, các nhà nghiên cứu cũng được hưởng lợi từ hiệu quả cao trong ước lượng tham số, được thể hiện ở độ nhạy thống kê (statistical power) lớn hơn so với phương pháp CB - SEM. Độ nhạy thống kê lớn hơn có nghĩa là PLS-SEM có nhiều khả năng nêu ra mối quan hệ đặc biệt có ý nghĩa khi nó thực sự có ý nghĩa thực tế trong tổng thể. Điều này cũng tương tự với các hồi quy dựa trên điểm tổng, bị tụt hậu so với PLS-SEM về mặt độ nhạy thống kê (Thiele và cộng sự, 2015)

               Tuy nhiên, PLS-SEM cũng có một số hạn chế. Kỹ thuật này không thể áp dụng khi mô hình 

cấu trúc chứa các vòng lặp nhân quả hoặc các mối quan hệ vòng tròn giữa các biến tiềm ẩn. Các mở 

rộng của thuật toán PLS-SEM cơ bản chưa được thực hiện trong các gói phần mềm PLS-SEM thông 

thường, tuy nhiên, vẫn cho phép xử lý mối quan hệ vòng tròn (Lohmoller, 1989). Hơn nữa, vì 

PLS-SEM không thiết lập đo lường mức độ phù hợp mô hình, nên việc sử dụng nó để kiểm định và

khẳng định lý thuyết là có giới hạn. Tuy nhiên, những nghiên cứu gần đây đã bắt đầu phát triển đo 

lường sự phù hợp với mô hình trong PLS-SEM, vì vậy mở rộng khả năng của phương pháp này

 (ví dụ Bentler và Huang, 2014). Chẳng hạn như Henseler và cộng sự (2014) đã giới thiệu chỉ số căn 

bậc hai phần dư trung bình chuẩn hóa - Standardized root mean square residual (SRMR), đo sự 

chênh lệch bình phương giữa các mối quan hệ quan sát được và tương quan mô hình, như một phương 

tiện để xác nhận giá trị một mô hình. Phương pháp này cũng đã được thực hiện trong phần mềm 

SmartPLS 3 và sẽ được thảo luận trong phần đánh giá mô hình cấu trúc trong Chương 6. Một đặc điểm

 khác của PLS-SEM là các ước lượng tham số không tối ưu về tính nhất quán, được gọi là PLS-SEM 

chệch (Chương 3). Mặc dù CB-SEM chủ trương nhấn mạnh sự khác biệt này giữa hai phương pháp, 

các nghiên cứu mô phỏng cho thấy rằng sự khác biệt giữa ước lượng CB-SEM và PLS-SEM là rất nhỏ 

khi các mô hình đo lường đạt được tiêu chuẩn tối thiểu được đề nghị về số lượng nhân tố và hệ số tải 

nhân tố. Cụ thể, khi các mô hình đo lường có bốn hoặc nhiều nhân tố và hệ số tải nhân tố đáp ứng các 

tiêu chuẩn chung (>=0.70), thì thực tế không có sự khác biệt giữa hai phương pháp về độ chính xác của

 tham số (ví dụ, Reinartz, Haenlein, và Henseler, 2009; Thiele và cộng sự, 2015). Do đó, sai chệch 

PLS-SEM được thảo luận rộng rãi không phù hợp thực tế đối với phần lớn các ứng dụng 

(ví dụ Binz Astrachan, Patel, và Wanzenried, 2014). Quan trọng hơn, sự khác biệt của các ước lượng

 tham số của PLS-SEM không nên được coi là chệch, nhưng đưa ra một kết quả khác biệt từ cách xử lý

 khác nhau của các phương pháp về cách đo lường khái niệm (các yếu tố chung so với tổng hợp). 

Hơn nữa, các nghiên cứu gần đây đã phát triển những sửa đổi của thuật toán PLS-SEM ban đầu, 

phù hợp với sự khác biệt PLS-SEM. Đáng chú ý nhất, phương pháp tiếp cận PLS nhất quán (PLSc) 

của Dijkstra và Henseler (2015a, 2015b) cung cấp ước lượng mô hình chính xác trong khi duy trì tất cả

 các điểm mạnh của phương pháp PLS, chẳng hạn như khả năng xử lý các mô hình phức tạp khi kích

 thước mẫu bị hạn chế, khái niệm đo lường nguyên nhân và các mối quan hệ phi tuyến (đối với một 

cách tiếp cận khác, xem Bentler và Huang, 2014). 

Tại https://www.smartpls.com/documentation/pls-sem-compared-with-cb-sem, chúng tôi cung cấp 

một ước tính so sánh của mô hình chấp nhận công nghệ cao (TAM, Davis, 1989) sử dụng PLS, PLSc

 và các CB-SEM dựa trên ước tính về khả năng sự phù hợp cực đại. So sánh cho thấy rằng PLS, PLSc,

 và CB-SEM dựa trên khả năng xác suất tối đa có tính tương ứng chặt chẽ, trong khi các công cụ ước 

lượng CB-SEM thay thế khác mang lại nhiều kết quả khác nhau.

Trong những trường hợp nhất định, đặc biệt khi có một chút kiến thức nền tảng về các mối quan hệ 

mô hình cấu trúc hoặc các phép đo lường khái niệm nghiên cứu hoặc khi nhấn mạnh hơn vào việc 

khám phá hơn là khẳng định, PLS-SEM là một thay thế hấp dẫn hơn so với CB-SEM. Hơn nữa, khi 

giả định CB-SEM bị vi phạm về mặt phân phối chuẩn, kích cỡ mẫu tối thiểu, và mô hình phức tạp tối 

đa, hoặc bất thường về phương pháp luận liên quan xảy ra trong quá trình ước lượng mô hình, 

PLS-SEM là một phương pháp thay thế tốt để kiểm định lý thuyết. 

Bảng 1.6 trình bày quy tắc kinh nghiệm hay còn gọi là quy tắc kinh nghiệm (rules of thumb), 

có thể được áp dụng khi quyết định sử dụng CB-SEM hoặc PLS-SEM. Có thể thấy, PLS-SEM 

không được khuyến cáo như là một thay thế phổ biến cho CB-SEM. Cả hai phương pháp khác nhau 

ở quan điểm thống kê, được thiết kế để đạt các mục tiêu khác nhau, và dựa vào các triết lý đo lường 

khác nhau. Do đó không phải kỹ thuật này cao hơn hẳn kỹ thuật kia và không phải kỹ thuật nào 

cũng thích hợp cho tất cả các tình huống. Nói chung, thế mạnh của PLS-SEM là điểm yếu

 của CB-SEM, và ngược lại. Điều quan trọng là các nhà nghiên cứu phải hiểu được các ứng dụng 

khác nhau của mỗi phương pháp để triển khai và sử dụng chúng cho phù hợp. Các nhà nghiên cứu 

cần áp dụng các kỹ thuật SEM trong trường hợp phù hợp nhất với mục tiêu nghiên cứu, đặc điểm 

dữ liệu, và thiết lập mô hình của họ (xem Roldan và Sanchez-Franco, 2012 để nắm chi tiết hơn).

BẢNG 1.5	Đặc điểm chính của PLS-SEM
Những đặc điểm dữ liệu
Kích thước mẫu	·         Không có các vấn đề nhận dạng với các kích thước mẫu nhỏ ·         Các thống kê nói chung đạt độ nhạy thống kê cấp độ cao với những kích thước mẫu nhỏ. ·         Các kích thước mẫu lớn tăng độ chính xác (ví dụ, tính nhất quán) của ước lượng PLS-SEM.
Sự phân phối	·         Không có sự giả định phân phối; PLS-SEM là phương pháp phi tham số.
Các giá trị khuyết	·         Các giá trị khuyết rõ rệt đều ở cấp độ thấp hơn mức hợp lý.
Thang đo lường	·         Làm việc với dữ liệu tham số, dữ liệu gần như là tham số (thứ bậc) và các biến được mã hóa nhị phân (với các hạn chế nhất định). ·         Có vài hạn chế khi sử dụng dữ liệu phân loại để đo lường các biến tiềm ẩn nội sinh.
Những đặc điểm mô hình
Số lượng biến quan sát trong từng mô hình đo lường khái niệm nghiên cứu	·         Đo lường khái niệm với đo lường đơn biến và đa biến
Các mối quan hệ giữa các khái niệm nghiên cứu và các biến quan sát của chúng	·         Dễ dàng kết hợp các mô hình đo lường nguyên nhân và kết quả.
Độ phức tạp mô hình	·         Xử lý các mô hình phức tạp với nhiều mối quan hệ mô hình cấu trúc
Thiết lập mô hình	·         Không vòng lặp nhân quả nào được cho phép trong mô hình cấu trúc
Đặc tính thuật toán của PLS-SEM
Mục tiêu	·         Giảm thiểu phương sai không giải thích được (tức là, tối đa giá trị R2)
Hiệu quả	·         Hội tụ sau khi lặp đi lặp lại (thậm chí trong các tình huống với mô hình phức tạp và/ hoặc tập hợp dữ liệu lớn) để đưa ra giải pháp tối ưu; thuật toán hiệu quả
Bản chất của khái niệm nghiên cứu	·         Được xem như là các đại diện của khái niệm tiềm ẩn được điều tra, được đại diện bởi các biến tổng hợp
Điểm số của khái niệm	·         Ước lượng các tổ hợp tuyến tính của các biến quan sát ·         Được xác định ·         Sử dụng cho mục đích dự đoán ·         Có thể sử dụng như đầu vào cho phân tích tiếp theo ·         Không ảnh hưởng bởi sự thiếu dữ liệu
Ước lượng tham số	·         Các quan hệ của mô hình cấu trúc nhìn chung đều bị đánh giá thấp và các mối quan hệ của mô hình đo lường nhìn chung được đánh giá cao khi ước lượng dữ liệu từ những mô hình yếu tố chung ·         Tính nhất quán cao ·         Độ nhạy thống kê cao
Vấn đề đánh giá mô hình
Sự đánh giá mô hình tổng thể	·         Không có tiêu chí độ phù hợp mô hình
Sự đánh giá mô hình đo lường	·         Mô hình đo lường kết quả: độ tin cậy và giá trị được đánh giá thông qua nhiều tiêu chí ·         Mô hình đo lường nguyên nhân: đánh giá giá trị, mức ý nghĩa và sự liên quan của các trọng số quan sát, sự đa cộng tuyến
Sự đánh giá mô hình cấu trúc	·         Sự đa cộng tuyến giữa các tập khái niệm, mức ý nghĩa của hệ số đường dẫn, tiêu chí để đánh giá khả năng dự đoán của mô hình
Phân tích bổ sung	·         Phân tích ma trận hiệu suất tác động ·         Các ảnh hưởng trung gian ·         Các mô hình thành phần thứ bậc ·         Phân tích đa nhóm ·         Phát hiện và xử lý tính không đồng nhất không quan sát được ·         Sự bất biến mô hình đo lường ·         Các ảnh hưởng điều tiết

Nguồn: Điều chỉnh từ The Journal of Marketing Theory and Practice 19 (2) (Spring 2011), 139-151. Copyright© 2011 by M. E. Sharpe, Inc. Used by permission. All Rights Reserved. Not for reproduction.

Bảng 1.6 Quy tắc kinh nghiệm trong việc chọn lựa giữa PLS-SEM và CB-SEM

Sử dụng PLS-SEM khi ·         Mục đích là dự báo các khái niệm nghiên cứu mục tiêu hoặc xác định khái niệm nghiên cứu “dẫn đường”. ·         Khái niệm đo lường nguyên nhân là một phần của mô hình cấu trúc. Lưu ý rằng đo lường nguyên nhân cũng được sử dụng với CB-SEM, nhưng đòi hỏi thay đổi đặc tính kỹ thuật của mô hình (ví dụ, khái niệm nghiên cứu phải bao gồm cả biến quan sát nguyên nhân và kết quả để đáp ứng yêu cầu xác định). ·         Mô hình cấu trúc phức tạp (nhiều khái niệm và nhiều biến quan sát) ·         Kích thước mẫu nhỏ và/ hoặc dữ liệu không phải là phân phối chuẩn. ·         Có kế hoạch sử dụng điểm biến tiềm ẩn trong phân tích tiếp theo. Sử dụng CB-SEM khi ·         Mục đích là kiểm định lý thuyết, khẳng định lý thuyết, hoặc so sánh với các lý thuyết thay thế khác. ·         Phần sai số yêu cầu đặc điểm kỹ thuật bổ sung, như là hiệp phương sai ·         Mô hình cấu trúc có quan hệ vòng tròn ·         Nghiên cứu yêu cầu bộ tiêu chí đánh giá độ phù hợp mô hình.

Nguồn:Điều chỉnh từ The Journal of Marketing Theory and Practice 19 (2) (Spring 2011), 139-151. Copyright© 2011 by M. E. Sharpe, Inc. Used by permission. All Rights Reserved. Not for reproduction.

Các đặc điểm dữ liệu

Yêu cầu kích thước mẫu tối thiểu

Đặc điểm dữ liệu như là kích thước mẫu tối thiểu, dữ liệu không chuẩn và thang đo lường (tức là sử dụng các loại thang đo khác nhau) được xem như là lý do bắt đầu thông thường nhất trong việc áp dụng PLS-SEM (Hair, Sarstedt, Ringle và cộng sự, 2012; Henseler và cộng sự, 2009). Trong khi một vài lập luận nhất quán với khả năng của phương pháp, phần còn lại thì không. Ví dụ, kích thước mẫu nhỏ có lẽ thường bị lạm dụng nhất trong tranh luận với các nhà nghiên cứu sử dụng PLS-SEM với kích cỡ mẫu nhỏ không thể chấp nhận được (Goodhue, Lewis, và Thompson, 2012; Marcoulides và Saunders, 2006). Các nhà nghiên cứu thường tin rằng có một “ma thuật” nào đó trong phương pháp PLS-SEM cho phép họ sử dụng một mẫu rất nhỏ (ví dụ dưới 100) để có được các kết quả đại diện cho các tác động tồn tại trong một tổng thể của một vài triệu yếu tố hoặc cá nhân. Không có kỹ thuật phân tích đa biến nào, bao gồm PLS-SEM, có những khả năng “ma thuật” này. Tuy nhiên, kết quả của những sai lệch này đã dẫn đến chủ nghĩa hoài nghi nói chung về việc sử dụng PLS-SEM.

Một mẫu là một sự lựa chọn của các yếu tố hoặc các cá thể riêng lẻ từ một tổng thể lớn hơn. Các cá thể được lựa chọn cụ thể trong quá trình lấy mẫu để đại diện cho tổng thể. Một mẫu tốt nên phản ánh sự tương đồng và sự khác biệt được tìm thấy trong tổng thể để có thể suy ra từ mẫu (nhỏ) về đám đông (lớn) tổng thể. Do đó, quy mô tổng thể và đặc biệt biến thể của các biến số trong nghiên cứu ảnh hưởng đến kích cỡ mẫu được yêu cầu trong quá trình lấy mẫu. Ngoài ra, khi áp dụng các kỹ thuật phân tích đa biến, các khuynh hướng mang tính kỹ thuật của mẫu sẽ trở nên phù hợp. Kích thước mẫu tối thiểu sẽ bảo đảm rằng các kết quả của phương pháp thống kê như PLS-SEM có đủ độ nhạy thống kê. Trong những điều này, một kích cỡ mẫu không đủ có thể không tiết lộ một tác động đáng kể nào tồn tại trong tổng thể cơ bản (kết quả là gây ra sai lầm loại II). Hơn nữa, cỡ mẫu tối thiểu phải đảm bảo rằng các kết quả của phương pháp thống kê là mạnh mẽ và mô hình có thể khái quát được. Kích thước mẫu không đủ có thể dẫn đến các kết quả PLS-SEM có sự khác biệt lớn so với các mẫu khác. Sau đây, chúng tôi tập trung vào phương pháp PLS-SEM và các yêu cầu kỹ thuật của nó về kích thước mẫu tối thiểu.

Tính phức tạp nói chung của mô hình cấu trúc có ảnh hưởng một ít lên yêu cầu kích thước mẫu cho PLS-SEM. Lý do là thuật toán không tính toán tất cả các mối quan hệ trong mô hình cấu trúc trong cùng một lúc. Thay vào đó, nó sử dụng hồi quy OLS để ước lượng các mối quan hệ hồi quy riêng phần của mô hình. Hai nghiên cứu ban đầu đã đánh giá một cách hệ thống tính hiệu quả của PLS-SEM với các kích thước mẫu nhỏ và đã kết luận rằng nó thực hiện tốt (ví dụ Chin và Newsted, 1999; Hui và Wold, 1982). Gần đây hơn, nghiên cứu mô phỏng của Reinartz và cộng sự (2009) đã chỉ ra rằng PLS-SEM là sự lựa chọn tốt khi kích thước mẫu nhỏ. Hơn nữa, so với kỹ thuật dựa trên hiệp phương sai đối lập, PLS-SEM có độ nhạy thống kê cao hơn trong các trường hợp cấu trúc mô hình phức tạp hoặc các kích thước mẫu nhỏ. Tương tự, Henseler và cộng sự, (2014) cũng cho thấy các giải pháp có thể thu được với PLS-SEM khi các phương pháp khác không hội tụ hoặc các giải pháp không thể chấp nhận được. Ví dụ, những vấn đề thường bị gặp phải khi sử dụng CB-SEM trên những mô hình phức tạp, đặc biệt khi kích cỡ mẫu bị giới hạn. Tương tự, CB-SEM bị các vấn đề nhận dạng và hội tụ khi đo lường nguyên nhân xuất hiện (ví dụ, Diamantopoulos và Riefler, 2011).

Không may, vài nhà nghiên cứu tin rằng kích thước mẫu nhỏ không đóng vai trò đặc biệt trong ứng dụng PLS-SEM. Ý kiến này được thúc đẩy bởi quy tắc 10 lần (Barclay, Higgins, và Thompson, 1995), cho rằng kích thước mẫu nên bằng hoặc lớn hơn:

1. Mười (10) lần số lớn nhất của các biến quan sát nguyên nhân được sử dụng để đo lường khái niệm đơn, hoặc

2. Mười (10) lần số lớn nhất của đường dẫn cấu trúc hướng vào một khái niệm riêng biệt trong mô hình cấu trúc.

Quy tắc kinh nghiệm nói rằng kích thước mẫu tối thiểu nên bằng 10 lần số lớn nhất của mũi tên trong biến tiềm ẩn ở mọi vị trí trong mô hình cấu trúc PLS. Trong khi quy định 10 lần đề xuất chỉ dẫn sơ bộ về yêu cầu kích thước mẫu tối thiểu, PLS-SEM - cũng như các kỹ thuật thống kê khác - yêu cầu nhà nghiên cứu cân nhắc lại kích thước mẫu với nền tảng mô hình và đặc điểm dữ liệu (Hair, Ringle, và Sarstedt, 2011; Marcoulides và Chin, 2013). Đặc biệt, kích thước mẫu cần thiết nên được xác định bởi phân tích độ nhạy dựa trên một phần mô hình với số lượng lớn nhất của biến dự báo.

Vì những kiến nghị kích thước mẫu trong PLS-SEM cơ bản dựa trên đặc tính của hồi quy OLS, các nhà nghiên cứu có thể dựa trên các quy tắc kinh nghiệm khác được cung cấp bởi Cohen (1992) trong phân tích độ nhạy thống kê của ông cho nhiều mô hình hồi quy bội, cung cấp mô hình đo lường có thể chấp nhận được về mặt hệ số tải ngoài (ví dụ hệ số tải nên ở trên ngưỡng chung là 0.70). Cách khác, các nhà nghiên cứu có thể sử dụng các chương trình như G*Power (miễn phí tại trang http://www.psycho.uni-duesseldorf.de) để thực hiện phân tích độ nhạy cụ thể nhằm thiết lập mô hình.

Bảng 1.7 chỉ ra những yêu cầu cần thiết về kích thước mẫu tối thiếu để phát hiện giá trị R² nhỏ nhất: 0.10, 0.25, 0.50 và 0.75 ở bất cứ khái niệm biến nội sinh nào trong mô hình cấu trúc với mức ý nghĩa 1%, 5% và 10%, giả định chung việc sử dụng độ nhạy thống kê 80% và mức độ phức tạp cụ thể của mô hình PLS (tức là số lượng tối đa các điểm mũi tên tại một khái niệm nghiên cứu trong mô hình PLS). Ví dụ, khi số lượng tối đa biến độc lập trong mô hình đo lường và mô hình cấu trúc là 5 (năm), sẽ cần 45 quan sát để đạt được độ nhạy thống kê 80%  cho việc phát hiện giá trị R² nhỏ nhất 0.25 (với 5% xác suất sai số).

Đặc điểm dữ liệu

Như mọi phân tích thống kê khác, các dữ liệu khuyết đều được xử lý khi sử dụng PLS-SEM. Đối với những giới hạn hợp lý (tức là, ít hơn 5% giá trị khuyết trên một quan sát), giá trị khuyết sẽ được lựa chọn xử lý bằng cách thay thế giá trị trung bình, EM (Expectation-maximization - thuật toán tối đa hóa kỳ vọng), và các giá trị lân cận gần nhất (ví dụ Hair và cộng sự, 2010) kết quả thông thường chỉ khác một ít trong ước lượng PLS. Cách khác, các nhà nghiên cứu có thể lựa chọn xoá tất cả các quan sát có dữ liệu khuyết, tuy nhiên, sự biến đổi trong dữ liệu sẽ giảm và có thể gây nên sự thiên lệch khi các nhóm quan sát nhất định bị xoá một cách có hệ thống.

Việc sử dụng PLS-SEM có hai lợi thế chính liên quan đến đặc điểm dữ liệu (tức là phân phối và thang đo). Do đó, trong nhiều tình huống khó khăn và không thể đáp ứng được yêu cầu chặt chẽ của nhiều kỹ thuật đa biến truyền thống (ví dụ, phân phối dữ liệu dạng chuẩn), PLS-SEM là phương pháp thích hợp hơn. Tính linh hoạt của PLS-SEM được mô tả bằng tên “mô hình mềm”, được đặt ra bởi Wold (1982), người phát triển phương pháp này. Tuy nhiên, lưu ý ở đây, “mềm” chỉ do sự giả định phân phối và không đề cập đến khái niệm, mô hình, hoặc kỹ thuật ước lượng (Lohmӧller, 1989). Đặc tính thống kê của PLS-SEM cung cấp những ước lượng mô hình mạnh mẽ với dữ liệu có đặc tính phân phối chuẩn cũng như cực không chuẩn (tức là độ lệch/độ nhọn) (Reinartz và cộng sự, 2009; Ringle và cộng sự, 2009). Tuy nhiên, phải ghi nhớ, giá trị ngoại lai, và cộng tuyến làm ảnh hưởng tới hồi quy OLS trong PLS-SEM, và các nhà nghiên cứu nên đánh giá dữ liệu và các kết quả của những vấn đề này (Hair và cộng sự, 2010).

Thuật toán PLS-SEM nhìn chung đòi hỏi dữ liệu dạng số trên thang đo tỷ lệ hoặc thang đo khoảng đối với các quan sát trong mô hình đo lường. Nhưng phương pháp này cũng làm việc tốt với thang đo thứ bậc với điểm dữ liệu cách đều (ví dụ thang đo bán tham số - quasi-metric scale; Sarstedt và Mooi, 2014) và dữ liệu mã hoá nhị phân. Cách sử dụng dữ liệu mã hoá nhị phân thường bao gồm các biến kiểm soát phân loại hoặc các biến điều tiết trong mô hình PLS-SEM. Nói ngắn gọn, các biến được mã hoá giả (dummy) có thể được tính đến trong mô hình PLS-SEM nhưng đòi hỏi sự chú ý đặc biệt (xem trong ghi chú của Hair và cộng sự, 2012b) và không nên được sử dụng như là biến phụ thuộc cuối cùng. Bảng 1.8 tổng hợp các cân nhắc chính liên quan đến đặc điểm dữ liệu.

Bảng 1.8  Những cân nhắc về dữ liệu khi áp dụng PLS-SEM

·         Theo hướng dẫn sơ bộ, kích thước mẫu tối thiểu trong một phân tích PLS-SEM nên bằng hoặc lớn hơn (quy tắc 10 lần) như sau: (1) 10 lần số lớn nhất của các biến chỉ báo nguyên nhân được sử dụng để đo lường khái niệm đơn, hoặc (2) 10 lần số lớn nhất của đường dẫn cấu trúc hướng vào một khái niệm riêng biệt trong mô hình cấu trúc. Tuy nhiên, các nhà nghiên cứu nên làm theo các khuyến nghị phức tạp hơn như các khuyến cáo của Cohen (1992), cũng như độ nhạy thống kê và ảnh hưởng của kích cỡ đến kết quả. Ngoài ra, các nhà nghiên cứu nên chạy phân tích độ nhạy riêng biệt, sử dụng các chương trình như G*Power. ·         Với những tập dữ liệu lớn (N=250 và lớn hơn), kết quả của CB-SEM và PLS-SEM là rất tương đồng khi một số lượng thích hợp của các biến quan sát (4 hoặc nhiều hơn) được sử dụng để đo lường từng khái niệm (tính nhất quán càng lớn). ·         PLS-SEM có thể xử lý dữ liệu rất không chuẩn (Ví dụ., một mức độ cao của độ xiên) ·         Hầu hết các thủ tục xử lý giá trị khuyết (ví dụ: thay thế trung bình, xóa theo cặp, EM và lấy theo điểm gần nhất) được sử dụng cho các mức dữ liệu bị khuyết hợp lý (ít hơn 5% khuyết cho mỗi biến quan sát) với hiệu quả hạn chế đối với các kết quả phân tích. ·         PLS-SEM hoạt động với dữ liệu số, bán tham số và phân loại (ví dụ: mã hóa giả), mặc dù có một số hạn chế nhất định

Các đặc điểm mô hình

PLS-SEM rất linh hoạt trong tính chất mô hình của nó. Thuật toán PLS-SEM đòi hỏi tất cả các mô hình đều không cho phép có mối quan hệ vòng tròn hoặc vòng lặp các mối quan hệ giữa các biến tiềm ẩn trong mô hình cấu trúc. Trong khi mô hình có vòng lặp hiếm khi được định rõ ở nghiên cứu kinh doanh, các đặc điểm này làm giới hạn tính ứng dụng của PLS-SEM nếu mô hình như vậy được yêu cầu. Các yêu cầu đặc điểm mô hình khác đều bắt buộc khi sử dụng CB-SEM, như là giả định phân phối, đều không liên quan đến PLS-SEM.

Những khó khăn của mô hình đo lường là một trong những chướng ngại chính trong việc đạt được một giải pháp đối với CB-SEM. Thí dụ, ước lượng của những mô hình phức tạp với nhiều biến tiềm ẩn và/hoặc biến chỉ báo thường là không thể với CB-SEM. Ngược lại, PLS-SEM có thể được sử dụng trong nhiều tình huống vì không bị hạn chế bởi sự xác định và các vấn đề kỹ thuật khác. Việc cân nhắc mô hình đo lường kết quả và nguyên nhân là vấn đề chính trong việc áp dụng SEM. PLS-SEM có thể dễ dàng xử lý cả hai mô hình đo lường nguyên nhân và kết quả và được xem xét như cách tiếp cận ban đầu khi mô hình giả thuyết kết hợp với đo lường nguyên nhân. CB-SEM có thể chứa các biến chỉ báo nguyên nhân nhưng để đảm bảo tính xác định của mô hình, chúng phải theo các quy định kỹ thuật chi tiết riêng biệt (Diamantopoulos và Riefler, 2011). Thực tế, các yêu cầu thường ngăn chặn việc chạy phân tích như dự định ban đầu. Ngược lại, PLS-SEM không có nhiều yêu cầu, và xử lý được mô hình đo lường nguyên nhân mà không gặp phải bất kỳ hạn chế nào. Điều này cũng áp dụng cho các thiết lập mô hình, trong đó các khái niệm nội sinh được đo lường nguyên nhân. Khả năng áp dụng CB-SEM vào các thiết lập mô hình như vậy đã và đang là một cuộc tranh luận đáng kể (Cadogan và Lee, 2013, Rigdon, 2014a), nhưng do quá trình ước lượng nhiều bước của PLS-SEM (Chương 3), các phân chia đo lường từ ước lượng mô hình cấu trúc, mà việc đưa vào các khái niệm nội sinh được đo lường nguyên nhân không phải là một vấn đề trong PLS-SEM (Rigdon và cộng sự, 2014). Vấn đề khó khăn duy nhất là tồn tại hiện tượng cộng tuyến ở cấp độ cao giữa các biến quan sát của mô hình đo lường nguyên nhân.

Cuối cùng, PLS-SEM có khả năng ước lượng những mô hình rất phức tạp. Ví dụ, nếu giả định lý thuyết hoặc khái niệm hỗ trợ những mô hình lớn và dữ liệu đầy đủ có sẵn (tức là đáp ứng yêu cầu kích thước mẫu tối thiếu), PLS-SEM có thể xử lý các mô hình với hầu hết các kích thước mẫu, gồm hàng tá khái niệm nghiên cứu và hàng trăm biến quan sát. Theo Wold (1985), PLS-SEM hầu như không có “đối thủ” khi mô hình đường dẫn với các biến tiềm ẩn có mối quan hệ cấu trúc phức tạp (Chương 3). Bảng 1.9 tóm tắt những quy tắc kinh nghiệm đối với đặc điểm mô hình PLS-SEM.

Bảng 1.9 Những cân nhắc mô hình khi chọn PLS-SEM

·         Những yêu cầu về mô hình đo lường là khá linh hoạt. PLS-SEM có thể xử lý cả mô hình đo lường nguyên nhân và kết quả cũng như đo lường đơn biến mà không cần những yêu cầu bổ sung hay ép buộc nào. ·         Sự phức tạp của mô hình nhìn chung không phải là vấn đề đối với PLS-SEM. Miễn là các dữ liệu thích hợp đáp ứng các yêu cầu về cỡ mẫu tối thiểu, sự phức tạp của mô hình cấu trúc hầu như không bị giới hạn.

Tóm tắt từ: Hair, J., Hult, G., Ringle, C., & Sarstedt, M. (2017). A primer on partial least squares structural equation modeling (PLS-SEM) (2nd ed.). Los Angeles: SAGE.